Codility Lesson 3 TapeEquilibrium 나만의 풀이

문제

A non-empty array A consisting of N integers is given. Array A represents numbers on a tape.

Any integer P, such that 0 < P < N, splits this tape into two non-empty parts: A[0], A[1], ..., A[P − 1] and A[P], A[P + 1], ..., A[N − 1].

The difference between the two parts is the value of: |(A[0] + A[1] + ... + A[P − 1]) − (A[P] + A[P + 1] + ... + A[N − 1])|

In other words, it is the absolute difference between the sum of the first part and the sum of the second part.

For example, consider array A such that:

A[0] = 3 A[1] = 1 A[2] = 2 A[3] = 4 A[4] = 3

We can split this tape in four places:

• P = 1, difference = |3 − 10| = 7
• P = 2, difference = |4 − 9| = 5
• P = 3, difference = |6 − 7| = 1
• P = 4, difference = |10 − 3| = 7

Write a function:

def solution(A)

that, given a non-empty array A of N integers, returns the minimal difference that can be achieved.

For example, given:

A[0] = 3 A[1] = 1 A[2] = 2 A[3] = 4 A[4] = 3

the function should return 1, as explained above.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [2..100,000];
• each element of array A is an integer within the range [−1,000..1,000].

 

대충 해석하자면 비어있지 않은 배열 A에 N개의 정수가 주어져있다.

P는 0 < P < N 인 정수이고 P는 두 부분으로 분할한다. | (A[0]) - (A[1] + A[2] + ... + A[N-1]) |

P = 1 / A[0], A[1]~A[N-1]만큼 분할하므로 계산하면 7이 나온다. 이하 내용은 같음

N은 2부터 10만까지 주어지고

각 A 배열의 요수는 -1000~1000까지 들어있다.

 

첫 번째 시도

for문 한 번만 돌리니 당연히 O(N) 나오겠지? ㅋㅋ라고 생각하여 만들었던 코드

그래서 결과는요? 두구두구두구....

 

def solution(A):
    P = {}

    for i in range(len(A)-1):
        if i==0:
            P[i] = abs(sum(A[:i+1])-sum(A[i+1:]))

        elif i==len(A)-2:
            P[i] = abs(sum(A[:i+1])-sum(A[i+1:]))

        else:
            P[i] = abs(sum(A[:i+1])-sum(A[i+1:]))

    return min(P.values())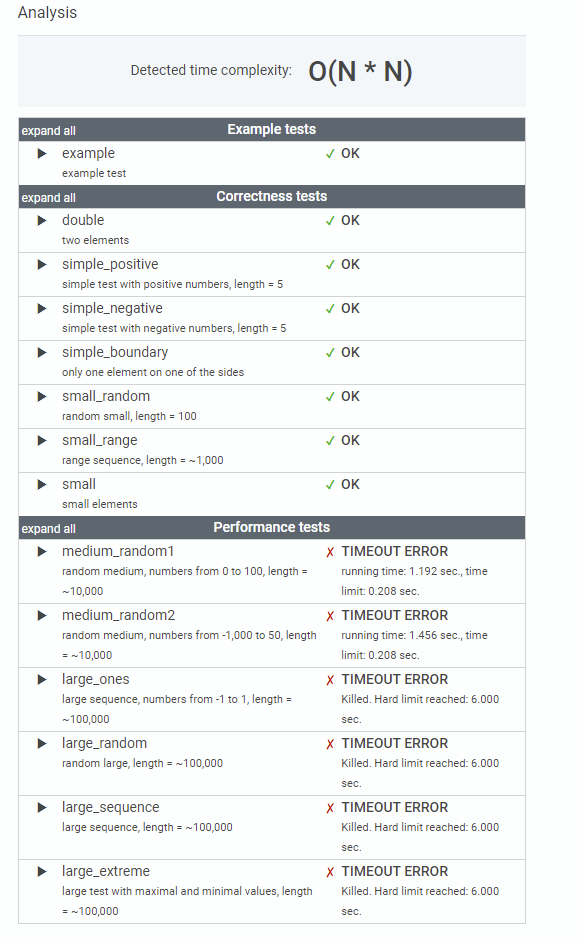

 

답은 맞았으나 성능 테스트에서 탈락한걸 볼 수있다. 점수는 53점

sum 함수도 배열만큼 돌아가서 최대 N-2번 돌린다는 걸 까먹고 있었다...

결론은 O(N²)으로 탈락!

 

 

두 번째 시도

곰곰이 생각을 해봤다

배열을 나눠서 sum을 하니까... 이중 for문이나 다름없잖아

왼쪽과 오른쪽으로 나뉜다고 치면 오른쪽의 요소가 왼쪽으로 한 개씩 이동한다

그렇다면 배열의 이동이 아닌 덧셈 뺄셈으로 할 수 있지 않을까?

해서 만든 코드

결과를 보자!

def solution(A):
    P = []
    start = A.pop(0)
    end = sum(A)
    index = 1

    while A:
        P.append(abs(start - end))
        val = A.pop(0)
        start += val
        end -= val
        index+=1

    return min(P)

 

 

여전한 O(N²)

배열의 이동을 뺐는데도 O(N²)이 나왔다.

다시 생각해보자

 

세 번째 시도

허... 대체 뭐가 문제지? 곰곰이 생각해봤더니

pop(0)을 하게 되면 N+번 배열이 N번으로 이동하는 문제가 발생하는 걸 생각을 안 했다!

그래서 A를 reverse 하여 pop()으로 배열의 방 이동 문제를 없애는 용도로 만들었다.

그리고 최솟값도 굳이 배열에 저장할 필요 없이 계속 min으로 최솟값을 가리는 코드로 넣었다.

그래서 결과는?

def solution(A):
    A.reverse()
    start = A.pop()
    end = sum(A)
    index = 1
    first = 500000000

    while A:
        P = abs(start - end)
        first = min([first, P])
        val = A.pop()
        start += val
        end -= val
        index+=1

    return first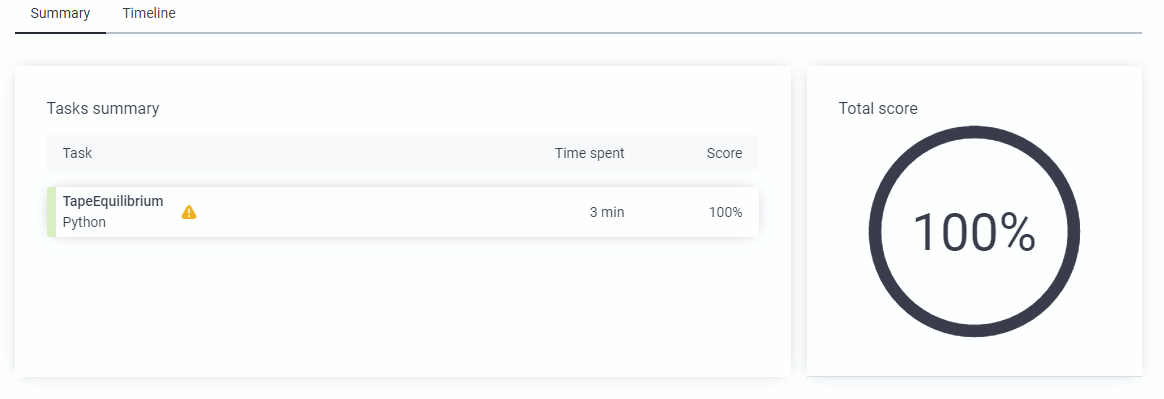

 

 

 

성공!!!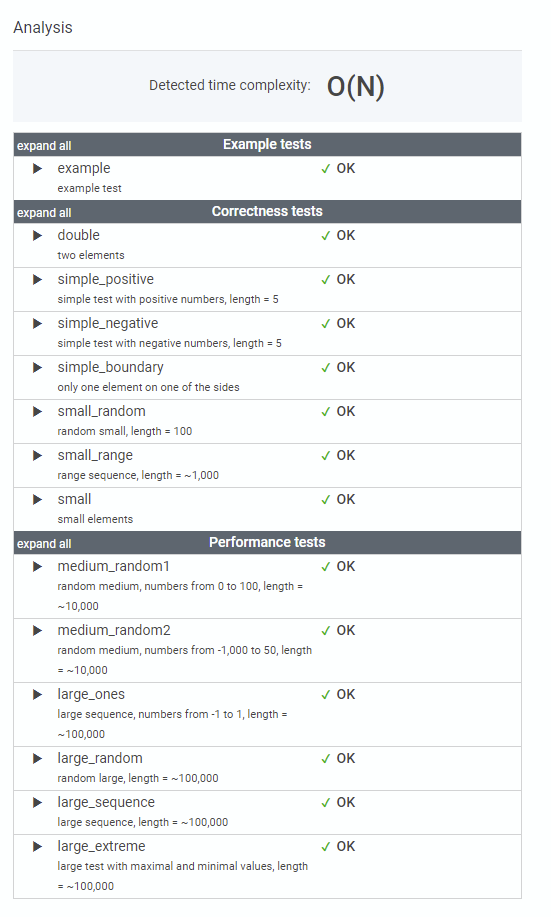

내 머릿속에서는 O(N)밖에 안 나오는데... 어떻게 더 줄일 방법이 있는지는 모르겠다.

large_extreme이 1.7초 나오던 게 최대 0.2초로 줄었다.

최대 허용 값은 0.7초 정도 가능하더라...